Graphic lambda calculus and chemlambda

By Jacques Bailhache ( jacques.bailhache@gmail.com ) June 2020

Graphic lambda calculus, chemlambda v1 (chemical concrete machine) and chemlambda v2 are successive versions of a graphical representation of an extension of lambda calculus related to emergent algebras, developed principally by Marius Buliga.

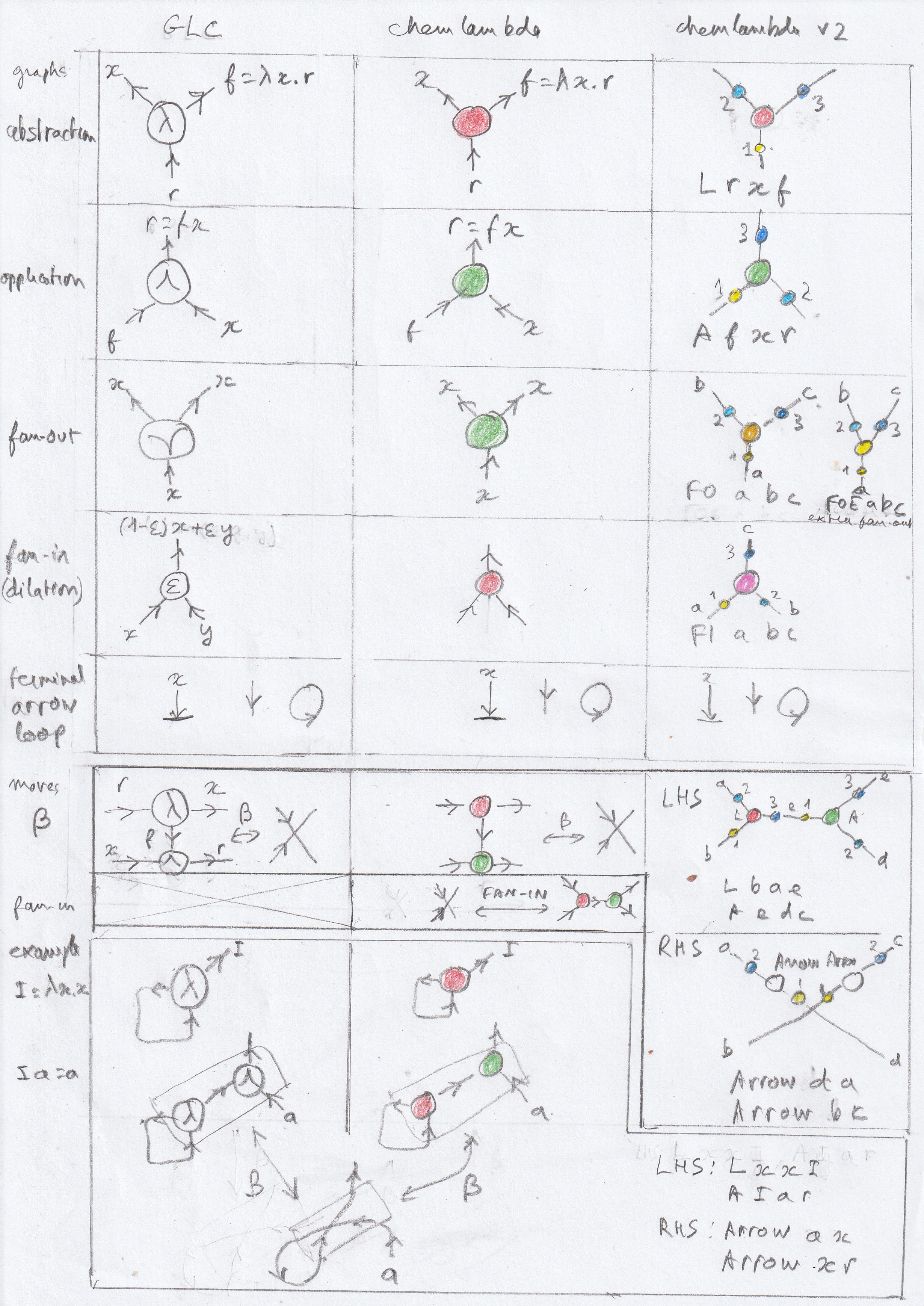
In the first version, graphic lambda calculus, there are the following elementary nodes called graphs or gates, labeled by different symbols (see picture) :

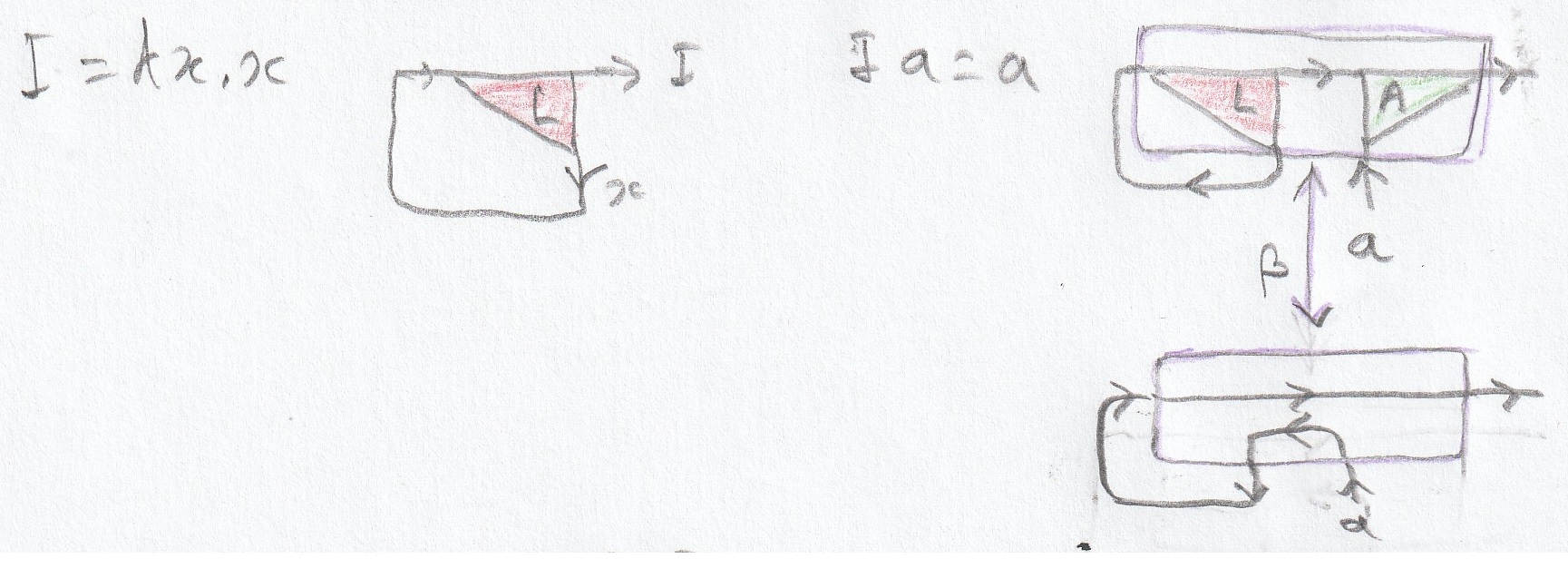
Abstraction : This gate defines a function. It has two outputs : the function being defined, and the variable, and one input : the result of the application of the function to the variable. Defining the function consists in conveniently connecting the variable to the result. For example, for the identity function I, the result is the variable itself, so we just have to connect directly the variable to the result.
Application : This gate has two input : a function, and the argument to which we want to apply the function, and one output, which is the result of the application of the function to the argument.
Fan-out : This gate has one input and two outputs which are the duplication of the input.
Fan-in : The meaning of this gate is more complex. It corresponds to an idempotent right quasigroup operation, which appears in emergent algebras as an abstraction of the geometrical operation of taking a dilation (of coefficient e), based at a point and applied to another point. Approximatively, if x and y are the input and e is the coefficient, then the output is something like x + e (y - x) = (1 - e) x + e y. However, the moves are compatible with this definition.
Terminal
Arrow
Loop

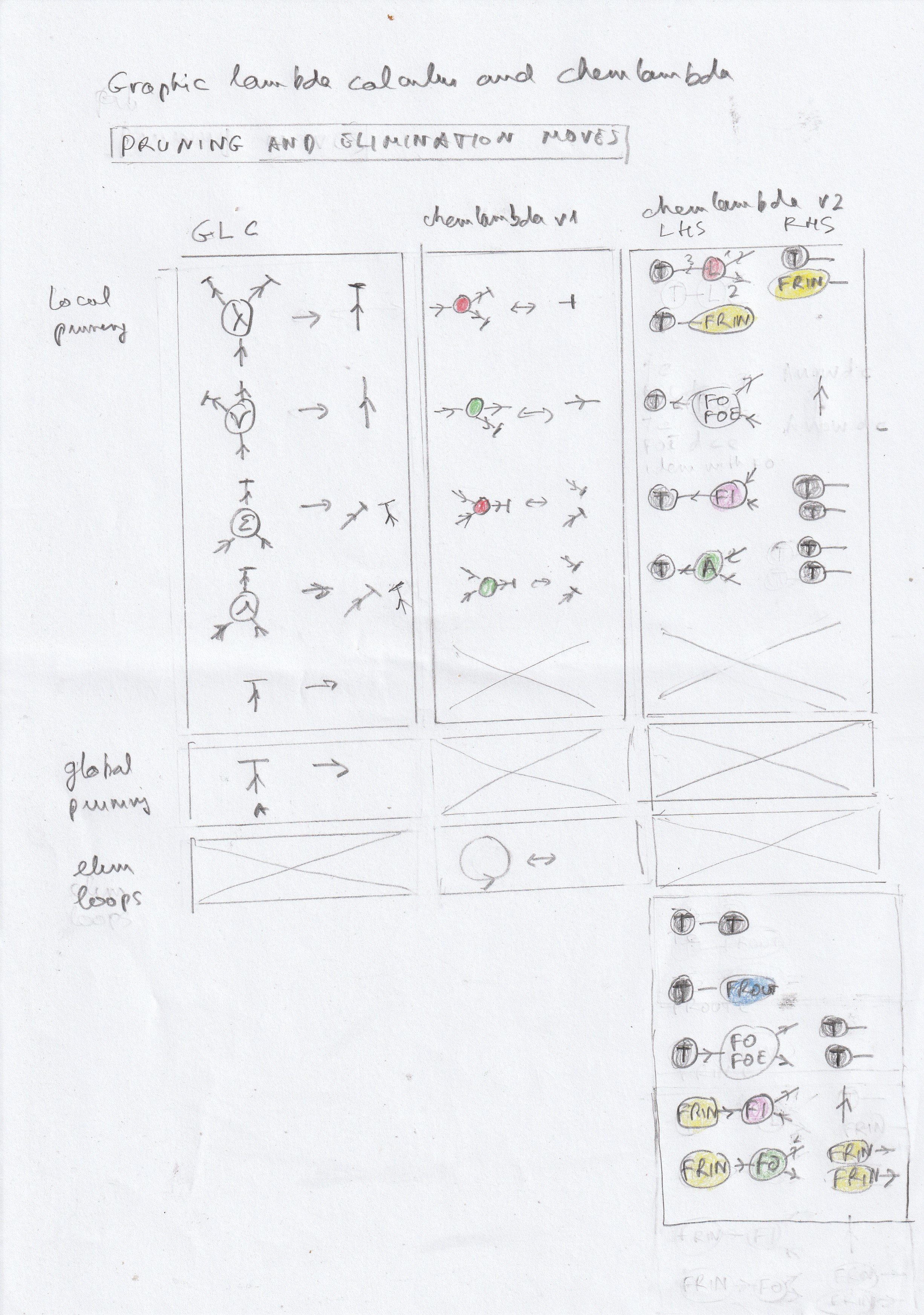
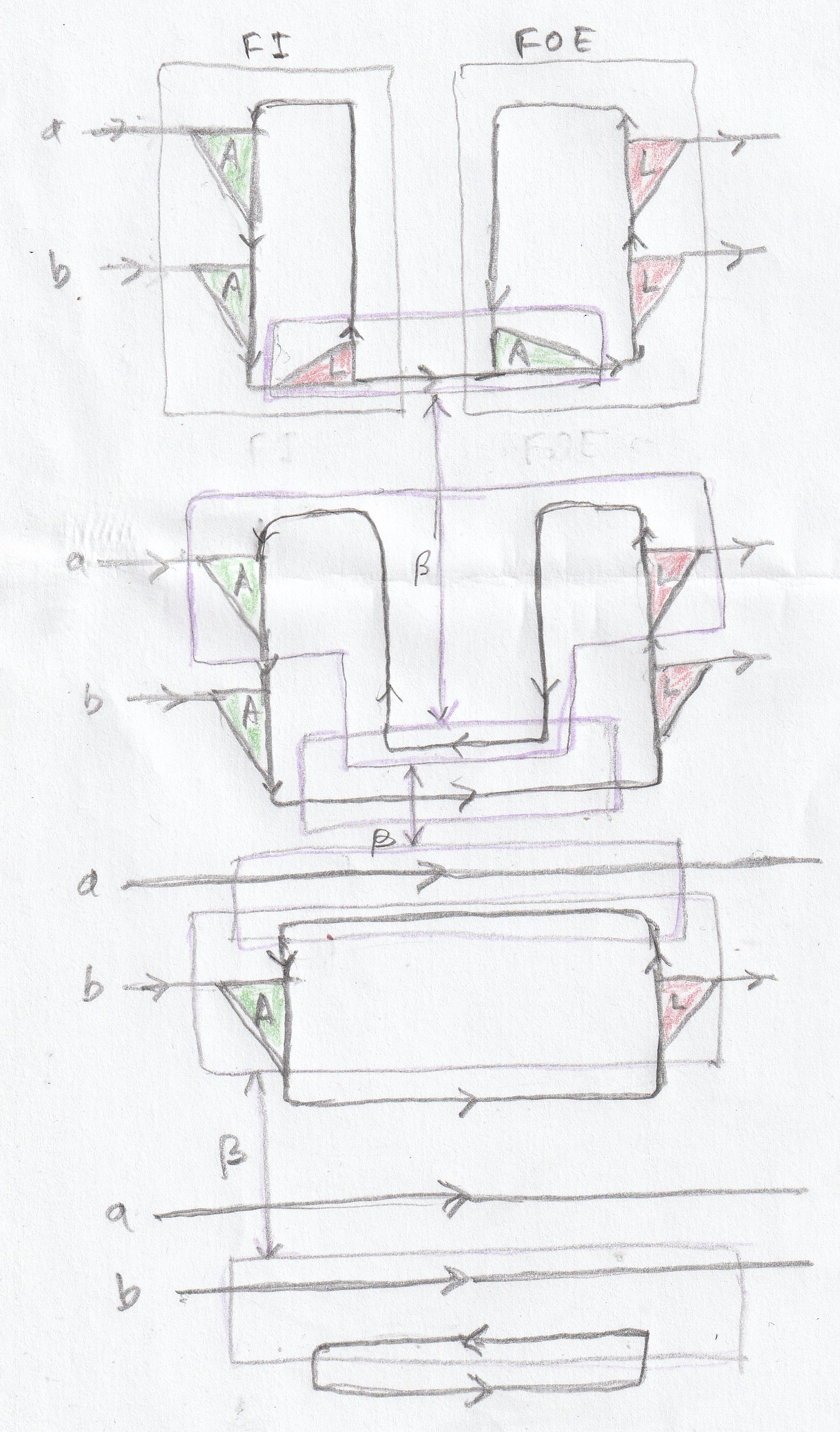
A set of graphical transformation rules called "moves" is define. An example of move is shown in the picture beside, with an example of reduction of a lambda calculus term.

In chemlambda v1, the symbols that label the gates are replaced by colors red and green (see picture). Gates with the same colors can be distinguished by the number of inputs and outputs. The GLC moves R1a, R1b, R2, Ext2 and Ext1 are removed and three new moves, FAN-IN and two DIST moves, are introduced. The FAN-IN move makes the meaning of fan-out gate more complex when combined with fan-in gate.

In chemlambda v2, different colors are used for the different gates, the input and output of the gates are numbered and represented by a small circle with different colors for the different inputs and outputs. A textual representation equivalent to the graphical representation is also defined.
The moves cocommutativity and coassociativity are removed, fan-out is called FOE (extra fan-out), and a new gate FO (fan-out) is introduced with new moves (DIST) for this gate.
We can see that we are consistent with the chemlambda v2 moves if we interpret FO as a gate that duplicates its input, FI as a gate that creates a pair from its two inputs (unless they are the same, in this case the output is the same as the inputs), and FOE as a gate that splits the input into its components if it is a pair, otherwise duplicates it like FO. Another possibility is to consider that the pair of x and x is the same as x.

The pictures below contain comparative tables of the moves in the different versions.

Evolution of the fan-in gate

In graphic lambda calculus, it is a gate labeled by a value e and we have seen that it can be interpreted as an arithmetical operation that, from two inputs x and y, produces the output (1 - e) x + e y. This definition is consistent with the moves cocommutativity, coassociativity, R1a, R1b, R2 and Ext2.
In chemlambda v2, the fan-in gate is no more labeled, and we have seen it can be interpreted as some kind of pairing operator. The moves cocommutativity, coassociativity, R1a, R1b, R2 and Ext2 have been replaced by FAN-IN and 6 DIST moves, which are consistent with the interpretation of a pairing operator.
In chemlambda v1, we have an intermediate situation without the moves R1a, R1b, R2, Ext2 but with stille the moves cocommutativity and coassociativity, and two DIST rules. The interpretation of the fan-in gate is not clear to me in this case.

Improving the theory

In chemlambda v2, the meaning of the FI (fan-in) and FOE gates are not very clear or complicated. It is like if the pair of an element with itself is considered as equal to this element, which is not traditionaly admitted. The FI gate seems to be a sort of pairing operator, but according to the moves it seems that when the two inputs are the same, the output is equal to the inputs. The FOE gate seems to be a pair splitting operator, but it seems that when applied to a non pair input, it duplicates its input like FO (fan-out). For FOE this is perhaps necessary if we want a "complete" operator that yields outputs for any input. But for FI, I don't see why we couldn't make a pair with an element and itself, distinguishing it from the initial element.

But, like in combinatory logic where we can define a pairing combinator as a combination of (I and) K and S, and in lambda calculus we can define a pairing function P such that P a b represents the pair <a,b>, with P a b c = c a b (a pair is a function that, when applied to another function, gives the result of the successive application of this other function to the elements of the pair) the same way we can define a pairing gate as a combination of other gates, so we don't need it as a primitive gate, and also we don't need the FOE gate since we can also define it as a combination of the other gates.

The main differences between the successive versions (graphic lambda calculus, chemlambda v1, chemlambda v2) are

the different meanings of the fan-in and fan-out gates
different graphical representations

If we remove the fan-in gate from any of this theory, and we keep only one fan-out which simply duplicates its input to two outputs, then we get a simpler and clearer theory.

The fan-out gate is necessary in graphic lambda calculus because one output cannot be connected to several inputs. If we remove this restriction, the fan-out gate is not needed.

Concerning the graphical representation, I thing there is no progress from graphic lambda calculus to chemlambda v1 : in graphic lambda calculus we can immediately identify the gate according to its label, but in chemlambda v1 it depends from the color and the number of inputs and outputs. Also in these two versions the order of the inputs and outputs is important so it limits the possibilities of graphical representation. Chemlambda v2 brings ameliorations, the labels come back beside the gates, the inputs and outputs are numbered, with a small colored circle, which permits free order, but it's complicated. A good representation should be simple, the gates should be easily identifiable, and the order of inputs and outputs should be free.

In the picture beside is an example of such a representation, with examples of abstraction and applicatin gates and beta move with comparison with graphic lambda calculus and chemlambda v1 and v2.

Below is an example of a graphical proof of the equality I a = a.

Pairing and splitting pair gates similar to FI and FOE in chemlambda v2 can be defined with abstraction and application gates as shown below (see also Packing and unpacking arrows in graphic lambda calculus).